tensopt
| download: tensopt_v3_122015.rar |
Animated example
Release notes for tensopt
Developers:
Fernando Fraternali(*) and Gerardo Carpentieri
University of Salerno, Italy
© Rel. 3.0 Dec. 2015 All Right Reserved
* corresponding author, f.fraternali@unisa.it
tensopt is a Matlab® code that performs the topology optimization of a tensegrity structure connecting a given set of nodes in 3D. It originates from a collaboration between Robert Skelton and Fernando Fraternali’s research group at the University of Salerno. The code examines all the possible connections between the given nodes (background structure), in the form of compressed members (“bars” or “struts”) and/or tensile elements (“strings” or “cables”). The optimal connectivity table is determined through a mass minimization algorithm, which accounts for multiple loading conditions; yield constraints; local buckling constraints in the compressed members; and a global stability constraint related to the magnitude of the minimum eigenvalue of the global stiffness matrix of the structure (eigmin). The buckling constraints are enforced by recourse to an iterative linear programming algorithm. The global stability constraint is instead enforced by penalizing the mass of solutions that exhibits eigmin lower than a given tolerance. The overall mass minimization algorithm is fully described in the following references:
NAGASE, K., SKELTON, R.E. Minimal mass tensegrity structures. JOURNAL OF THE INTERNATIONAL ASSOCIATION FOR SHELL AND SPATIAL STRUCTURES, 55 (1), 37-48, 2014.
SKELTON, R.E., FRATERNALI, F., CARPENTIERI, G., MICHELETTI, A.. Minimum mass design of tensegrity bridges with parametric architecture and multiscale complexity. MECHANICS RESEARCH COMMUNICATIONS, 58, 124-132, 2014.
FRATERNALI, F., CARPENTIERI, G., MODANO, M., FABBROCINO, F., SKELTON, R.E. A tensegrity approach to the optimal reinforcement of masonry domes and vaults through fiber-reinforced composite materials. COMPOSITE STRUCTURES, 134, 247-254, 2015.
CARPENTIERI, G., SKELTON, R.E., FRATERNALI, F. Minimum mass and optimal complexity of planar tensegrity bridges. INTERNATIONAL JOURNAL OF SPACE STRUCTURES, 30(3-4), 221-244, 2015.
The compressed file tensopt_v3_122015.rar (about 6.5 MB) includes the following subfolders:
main: providing a read_me file; the Matlab® code tensopt.m; the executable tensopt.exe for windows (for Matlab® users, not including the
Matlab® routines called by tensopt).
examples: providing input/output files for the illustrative examples shown in Fig. 1, and a Mathematica® codes (“MATHEMATICA_viewer“) that
visualizes the optimized structure.
papers: providing the above references.
The file tensopt0514_pkg.rar (about 160 MB) instead provides a compressed version of the Matlab® package tensopt_pkg.exe, which includes tensopt and the linked Matlab® routines. Download: tensopt_v3_pkg_122015.rar
Warning: If the number of nodes is too large, you might run out of memory, depending on the available memory.
Examples library
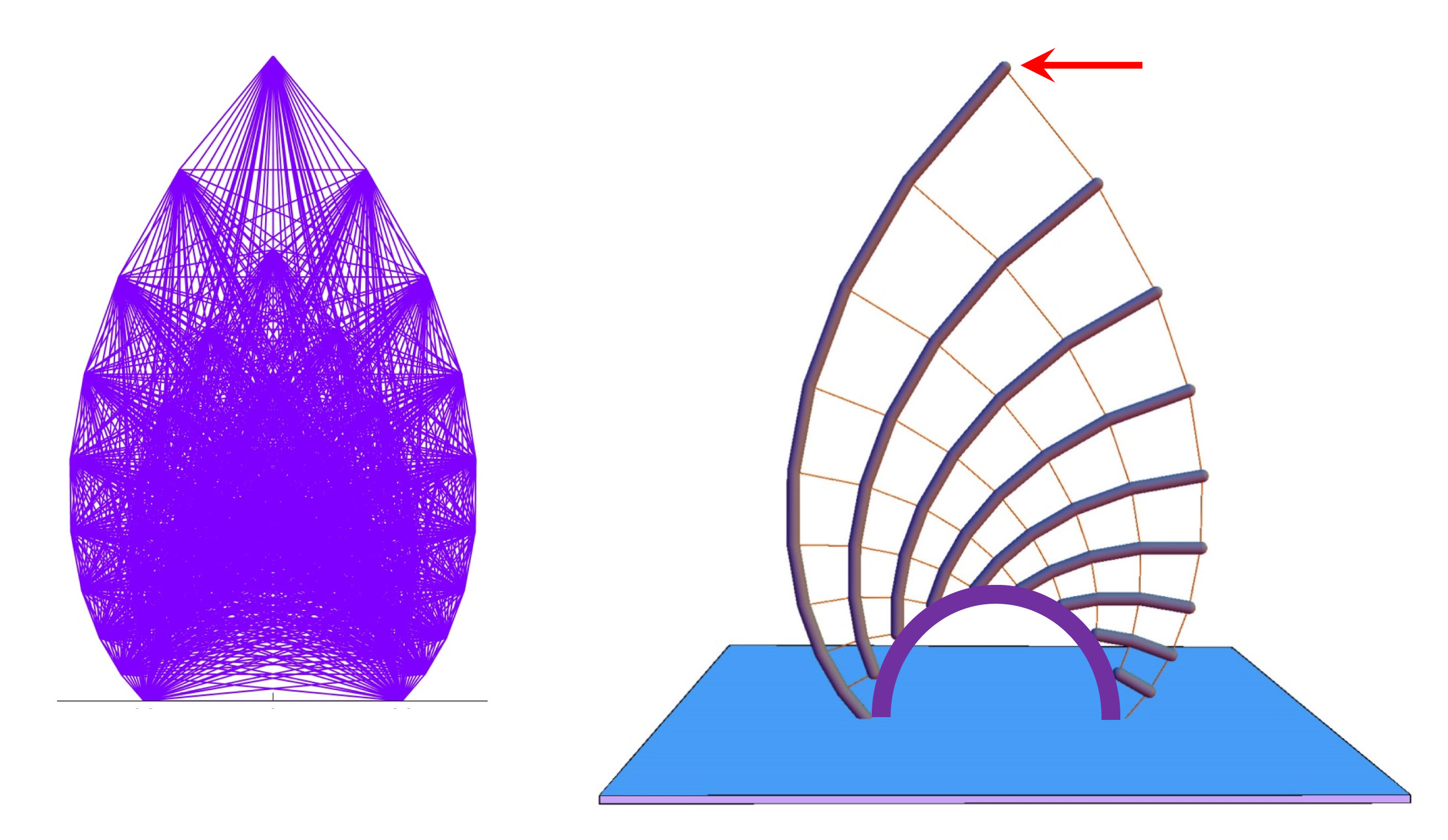
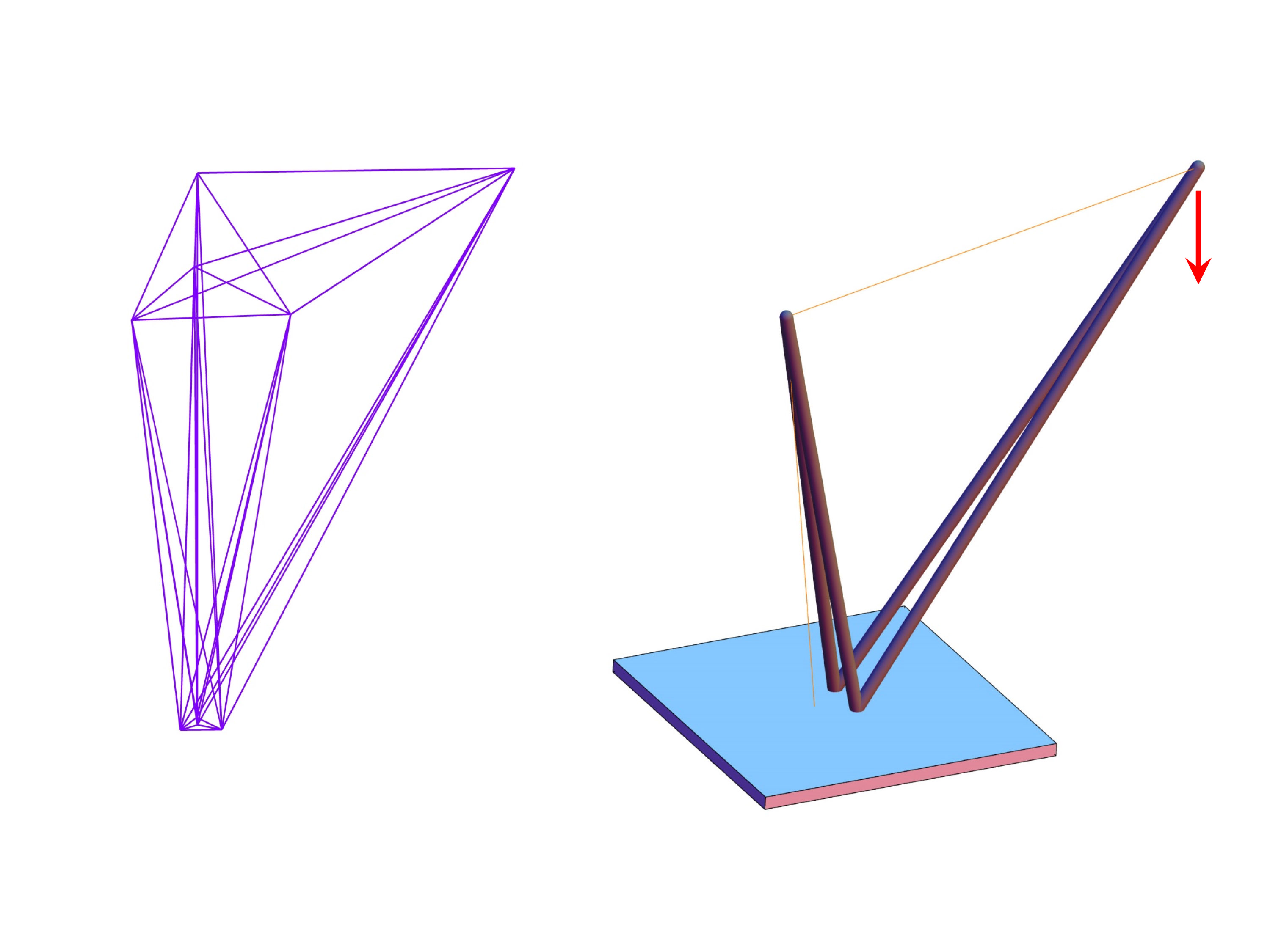
a) Example 1: Cantilever tensegrity ("Michell truss"). Left: background structure. Right: minimum mass structure.
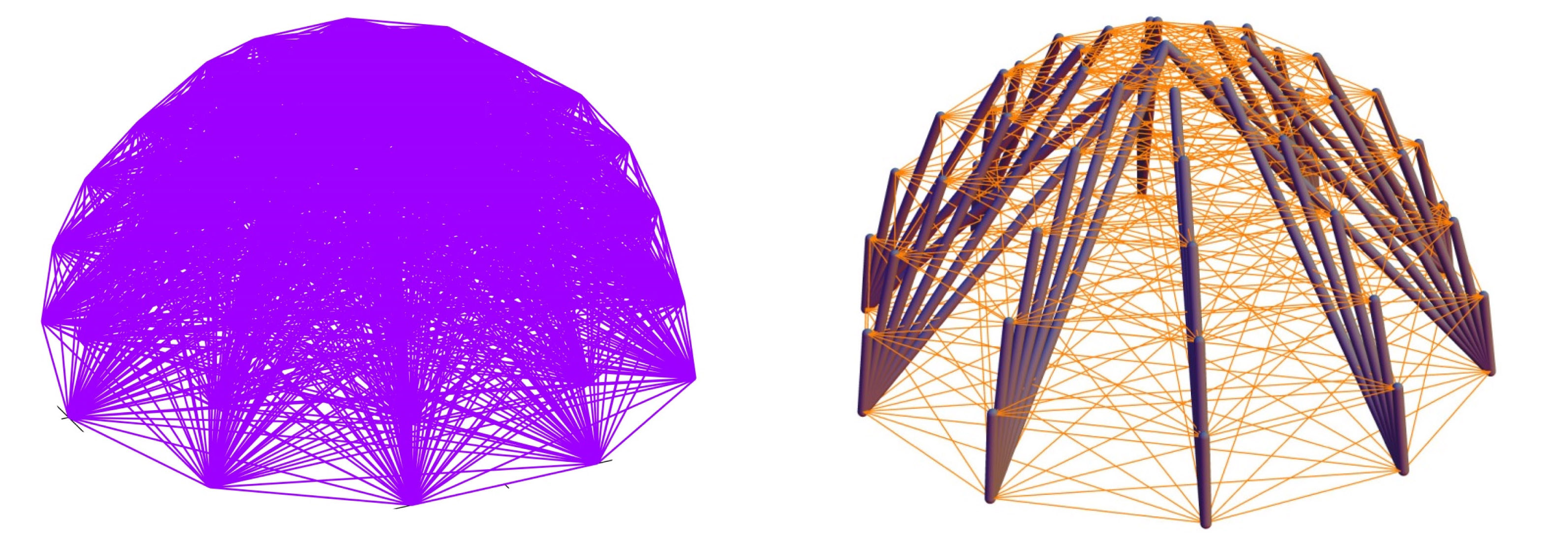
b) Example 2: Hemisphere tensegrity. Left: background structure. Right: minimum mass structure.
If you have examples to share on this page, please send them to: f.fraternali@unisa.it
Animation of the topology optimization of a cantilever structure (\mu denotes a dimensionless measure of the mass of the structure; the thick elements are the compressed struts, while the thin elements are the stretched cables).
Release notes for tensopt
Developers:
Fernando Fraternali(*) and Gerardo Carpentieri
University of Salerno, Italy
© Rel. 3.0 Dec. 2015 All Right Reserved
* corresponding author, f.fraternali@unisa.it
tensopt is a Matlab® code that performs the topology optimization of a tensegrity structure connecting a given set of nodes in 3D. It originates from a collaboration between Robert Skelton and Fernando Fraternali’s research group at the University of Salerno. The code examines all the possible connections between the given nodes (background structure), in the form of compressed members (“bars” or “struts”) and/or tensile elements (“strings” or “cables”). The optimal connectivity table is determined through a mass minimization algorithm, which accounts for multiple loading conditions; yield constraints; local buckling constraints in the compressed members; and a global stability constraint related to the magnitude of the minimum eigenvalue of the global stiffness matrix of the structure (eigmin). The buckling constraints are enforced by recourse to an iterative linear programming algorithm. The global stability constraint is instead enforced by penalizing the mass of solutions that exhibits eigmin lower than a given tolerance. The overall mass minimization algorithm is fully described in the following references:
NAGASE, K., SKELTON, R.E. Minimal mass tensegrity structures. JOURNAL OF THE INTERNATIONAL ASSOCIATION FOR SHELL AND SPATIAL STRUCTURES, 55 (1), 37-48, 2014.
SKELTON, R.E., FRATERNALI, F., CARPENTIERI, G., MICHELETTI, A.. Minimum mass design of tensegrity bridges with parametric architecture and multiscale complexity. MECHANICS RESEARCH COMMUNICATIONS, 58, 124-132, 2014.
FRATERNALI, F., CARPENTIERI, G., MODANO, M., FABBROCINO, F., SKELTON, R.E. A tensegrity approach to the optimal reinforcement of masonry domes and vaults through fiber-reinforced composite materials. COMPOSITE STRUCTURES, 134, 247-254, 2015.
CARPENTIERI, G., SKELTON, R.E., FRATERNALI, F. Minimum mass and optimal complexity of planar tensegrity bridges. INTERNATIONAL JOURNAL OF SPACE STRUCTURES, 30(3-4), 221-244, 2015.
The compressed file tensopt_v3_122015.rar (about 6.5 MB) includes the following subfolders:
The file tensopt0514_pkg.rar (about 160 MB) instead provides a compressed version of the Matlab® package tensopt_pkg.exe, which includes tensopt and the linked Matlab® routines. Download: tensopt_v3_pkg_122015.rar
Warning: If the number of nodes is too large, you might run out of memory, depending on the available memory.
Examples library

a) Example 1: Cantilever tensegrity ("Michell truss"). Left: background structure. Right: minimum mass structure.

b) Example 2: Hemisphere tensegrity. Left: background structure. Right: minimum mass structure.

If you have examples to share on this page, please send them to: f.fraternali@unisa.it